
円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学
またまた「小中学生にもわかる」シリーズだが、 今回は「錐体の体積は底面積×高さ÷3」 という公式についてである。 この公式は小学校高学年で教わることになっているが、 子供に 「なんで÷3かわかる?」 と聞くと、 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle
円錐の体積の公式
円錐の体積の公式- この記事の目的:錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する. はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると? 最後に 三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。

高さの分からない円すい展開図 どうやって立体の体積を求めるの
しかし,中学校の教科書には,これらの事実の証明は書かれ ていない。以下では,円柱の体積の公式と高校の「数学B」までの知識を使って, 円錐の体積の公式を導こう。 x2 円錐の体積 半径r の円を底面とする高さh の円錐K を考える。底面積はS = ˇr2 で 積分を用いて円錐の体積 を求める以下の公式を導出します. ここで, は底面の半径, は円錐の高さとします. 証明:まず,xy平面上に原点を通る直線を考えます.この直線とx軸とのなす角をθとすると,この直線は と表せます.この直線の式とx軸および2直線 および で囲まれた図形円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより円錐の体積が得られるのかを, 定積分法 と 区分求積法 を用いて説明する. ここで,説明に用いる円錐は f(x)= x f ( x) = x
体積の公式は? 体積の公式は、柱体(ちゅうたい)、錐体(すいたい)、球(きゅう)で式が違います。特に、柱体と錐体の体積の公式はよく使うので覚えましょうね。下記に示します。 柱体(ちゅうたい) ⇒ 底面積×高さ 円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です. なんかこれってモヤモヤしませんでしたか? おそらく中1で習ったはずなんですが,T:そうです。錐体を2倍に拡大します。相似な2倍の錐体の体積は8倍 つまり、錐体の体積は底面積と高さに比例するわけだから、錐体の体積=底面積×高さ×kです。(kは定数) これは、錐体の形によって体積が変わるのではなく、底面積と高さによっていることを示しているね。 4、円錐は三角錐の塊
円錐の体積の公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐の体積の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
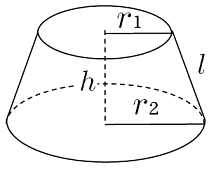
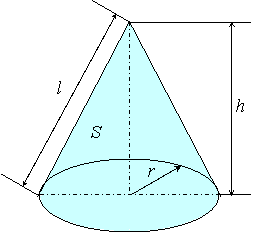
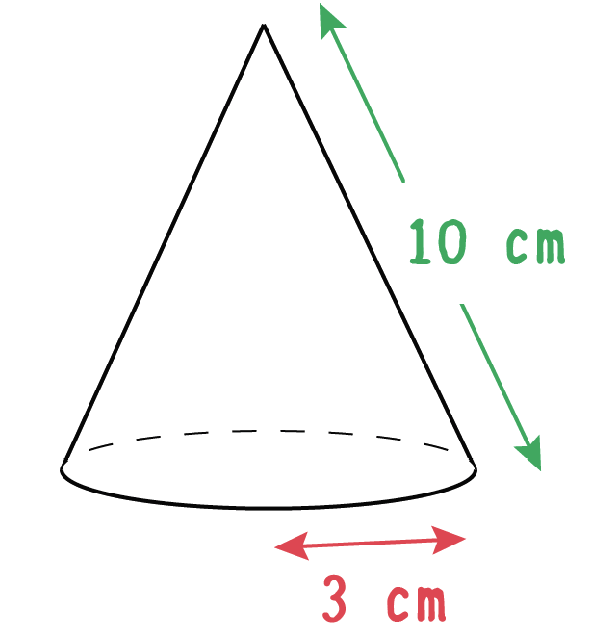
円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより 最初に円錐の体積の求め方の解説をします。 円錐の体積の公式は以下のようになっています。 円錐だけに限らず角錐(三角錐、四角錐など)の体積も「底面積×高さ×1/3」で求めることができましたね。 底面の円の半径をr、高さをhとすると、底面積は\(πr^2\)なので、 円錐の体積は \(\frac{1}{3}πr^2h\) と表すことができます。
Incoming Term: 円錐の体積の公式, 円錐の体積の公式証明,




0 件のコメント:
コメントを投稿